Digitale Dienste
Informationsportal
Hier bin ich:
Inhaltlich verantwortlich:
Steve Wohlfarth
Eingestellt am: 17.11.2022
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Steve Wohlfarth auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art42227)
Steve Wohlfarth auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art42227)
Die niveaubestimmenden Aufgaben im Fach Mathematik bilden in ihrer Gesamtheit wesentliche Aspekte des kompetenzorientierten Fachlehrplanes ab. Exemplarisch konkretisieren sie die Kompetenzentwicklung bezogen auf die Schuljahrgänge. Dabei werden inhaltsbezogene und allgemeine mathematische Kompetenzen in unterschiedlichen Anforderungsbereichen berücksichtigt. Die ausgewiesenen Hilfsmittel bieten eine Orientierung für die Unterrichtsarbeit und unterstützen die Forderungen des Fachlehrplanes zum einen nach einer vom Hilfsmittel unabhängigen Entwicklung der mathematischen Kompetenzen und zum anderen nach einem didaktisch begründeten und zieladäquaten Einsatz digitaler Werkzeuge.
|
Name und Art der Aufgabe |
Inhaltsbereiche |
Schuljahrgänge |
Hilfsmittel | Aufgabe | |
|
"Sechsstellige Zahlen" Lernaufgabe |
 |
5/6 | keine |  |
|
|
"Mannschaftsrechnen" Lernaufgabe |
|
|
5/6 | keine | |
|
"Dreiecke" Lernaufgabe |
 |
5/6 |
keine DMW möglich |
|
|
|
"Container" Leistungsaufgabe |
|
5/6 |
keine |
|
|
|
"Vitamin C" Leistungsaufgabe |
 |
5/6 |
keine |
|
|
|
"Taschengeld" Lernaufgabe |
|
5/6 |
keine |
|
|
Hauptschulabschlussbezogener Unterricht
|
Name und Art der Aufgabe |
Inhaltsbereiche |
Schuljahrgänge |
Hilfsmittel | Aufgabe | |
|
"Zuckerrüben" Lernaufgabe |
|
7/8 | WTR | |
|
|
"Wertvolle Variablen" Lernaufgabe |
|
7/8 |
WTR DMW möglich |
|
|
|
"Trapez" Lernaufgabe |
|
7/8 |
WTR |
|
|
|
"Münzen" Lernaufgabe |
|
|
7/8 |
WTR |
|
|
"Stromverbrauch" Lernaufgabe |
|
7/8 |
WTR DMW möglich |
|
|
|
"Verkehrskontrolle" Lernaufgabe |
 |
7/8 |
WTR DMW möglich |
|
|
|
"Internethandel" Lernaufgabe |
|
9 |
WTR |
|
|
|
"Elementares - hilfsmittelfrei, schnell und richtig" |
keine |
|
|||
Realschulabschlussbezogener Unterricht
|
Name und Art der Aufgabe |
Inhaltsbereiche |
Schuljahrgänge |
Hilfsmittel | Aufgabe | |
|
"Zuckerrüben" Lernaufgabe |
|
7/8 | WTR | |
|
|
"Wertvolle Variablen" Lernaufgabe |
|
7/8 |
WTR DMW möglich |
|
|
|
"Trapez" Lernaufgabe |
|
7/8 |
WTR |
|
|
|
"Münzen" Lernaufgabe |
|
|
7/8 |
WTR |
|
|
"Temperaturskalen" Leistungsaufgabe |
|
7/8 |
WTR |
|
|
|
"Verkehrskontrolle" Lernaufgabe |
|
7/8 |
WTR DMW möglich |
|
|
|
"Magdeburger Türme" Lernaufgabe |
|
9/10 |
WTR |
|
|
|
"Bauständer" Leistungsaufgabe |
|
9/10 |
WTR |
|
|
|
"Funktionenmix" Lernaufgabe |
|
9/10 |
WTR DMW möglich |
|
|
|
"Fahrradtour" Leistungsaufgabe |
|
|
9/10 |
WTR |
|
|
"Flughafenkontrollen" Lernaufgabe |
|
9/10 |
WTR |
|
|
|
"Elementares - hilfsmittelfrei, schnell und richtig" |
keine |
|
|||
Inhaltlich verantwortlich:
Aniko Riebenstahl, Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg)
Eingestellt am: 25.09.2020
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39806)
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39806)
Lizenzangaben der eingebundenen Medien
 | Originalbild von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
 | Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
Beitrag eingestellt von: Frau Aniko Riebenstahl
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
| Niveaubestimmende Aufgabe Sekundarschule | Mathematik |
| Schuljahrgänge 5/6 | |
| Fachlehrplan | Geometrische Grundbegriffe und Symmetrie; Dreiecke |
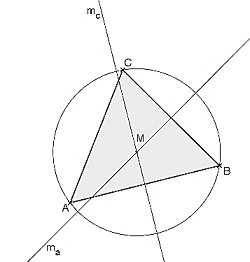
Umkreis eines Dreiecks
|
| KMK-Strategie Bildung in der digitalen Welt |
5.2. Werkzeuge bedarfsgerecht einsetzen |
|
| Aufgabentyp | Lernaufgabe | |
| Zeit | 45 Minuten | |
| Produkt |
Ergebnisprotokoll |
|
| Medien | PC oder Tablet mit zugehörigem Programm (z. B. GeoGebra) oder App für jeden Lernenden | |
| Aufgabenbeschreibung |
Ausführung von Konstruktionen mit DMW Untersuchung des Zusammenhanges Dreiecksart und Lage des Umkreismittelpunktes |
|
|
Did. Hinweise
|
Aufgabe
|
|
Inhaltlich verantwortlich:
Aniko Riebenstahl, Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg)
Eingestellt am: 25.09.2020
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39807)
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39807)
Lizenzangaben der eingebundenen Medien
 | Originalbild von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
Beitrag eingestellt von: Frau Aniko Riebenstahl
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
| Niveaubestimmende Aufgabe Sekundarschule | Mathematik |
| Schuljahrgänge 7/8 |
|
| Fachlehrplan | Kreis |
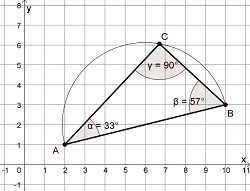
Satz des Thales
|
| KMK-Strategie Bildung in der digitalen Welt |
5.2. Werkzeuge bedarfsgerecht einsetzen |
|
| Aufgabentyp | Lernaufgabe | |
| Zeit | 45 Minuten | |
| Produkt |
Ergebnisprotokoll/Kopiervorlage |
|
| Medien | PC oder Tablet mit zugehörigem Programm (z. B. GeoGebra) oder App für jeden Lernenden | |
| Aufgabenbeschreibung |
Ausführung von Konstruktionen mit DMW Untersuchung der Winkel im rechtwinkligen Dreieck, bei dem die längste Seite der Durchmesser eines Kreises ist Entdeckung Satz des Thales
|
|
|
Did. Hinweise
|
Aufgabe
|
|
Inhaltlich verantwortlich:
Aniko Riebenstahl, Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg)
Eingestellt am: 25.09.2020
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39808)
Petra Behling (Halle),PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39808)
Lizenzangaben der eingebundenen Medien
 | Originalbild von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
Beitrag eingestellt von: Frau Aniko Riebenstahl
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
Telefon: 0345 2042215
E-Mail: aniko.riebenstahl@sachsen-anhalt.de
| Niveaubestimmende Aufgabe Sekundarschule | Mathematik |
| Schuljahrgänge 9/10 |
|
| Fachlehrplan | Daten und Zufall – Häufigkeitsverteilungen |
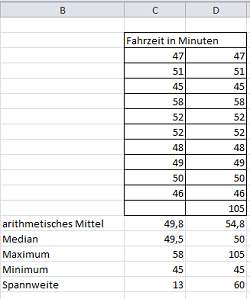
Lage- und Streumaße von Häufigkeitsverteilungen
|
| KMK-Strategie Bildung in der digitalen Welt |
5.2 Werkzeuge bedarfsgerecht einsetzen 1.2 Auswerten und Bewerten |
|
| Aufgabentyp | Prüfungsaufgabe | |
| Zeit | 30 Minuten | |
| Produkt |
Testergebnis |
|
| Medien |
digitales Mathematikwerkzeug für jeden Lernenden (Tabellenkalkulation) |
|
| Aufgabenbeschreibung |
Diese Modellierungsaufgabe zielt darauf ab, grundlegende Kenngrößen unter Nutzung digitaler Werkzeuge zu berechnen und zu interpretieren. Dazu zählen die Berechnung des arithmetischen Mittels sowie von Spannweite und Median sowie deren Interpretation in der Realsituation. Weiterhin muss analysiert werden, ob Durchschnitt (arithmetisches Mittel) und Median zur Beschreibung geeignet sind und die Lernenden müssen die Folgen von Ausreißern im Hinblick auf arithmetisches Mittel und Median beurteilen können. |
|
|
Did. Hinweise
|
Aufgabe
|
Material (Kopiervorlage)
|
Inhaltlich verantwortlich:
Andrea Neubauer, Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg)
Eingestellt am: 22.09.2020
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39791)
Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39791)
Lizenzangaben der eingebundenen Medien
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
 | Originalbild von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
Beitrag eingestellt von: Frau Andrea Neubauer
Telefon: +49 (0)345 2042 264
E-Mail: andrea.neubauer@sachsen-anhalt.de
Telefon: +49 (0)345 2042 264
E-Mail: andrea.neubauer@sachsen-anhalt.de
| Niveaubestimmende Aufgabe Sekundarschule | Mathematik |
| Schuljahrgang 10 | |
| Fachlehrplan | Quadratische Gleichung, quadratische Funktion, Sinusfunktion |
Hängebrücke
|
| KMK-Strategie Bildung in der digitalen Welt | 5.2 Werkzeuge bedarfsgerecht einsetzen | |
| Aufgabentyp | Prüfungsaufgabe | |
| Zeit | 30 Minuten | |
| Produkt |
Dokumentation auf einem Arbeitsblatt |
|
| Medien |
Wissenschaftlicher Taschenrechner |
|
| Aufgabenbeschreibung |
Exemplarisch illustriert diese Aufgabe eine einfache Modellierung eines realen Sachverhalts. Eine erfolgreiche Bearbeitung setzt voraus, dass die Eigenschaften quadratischer Funktionen sowie zugehörige Untersuchungsmethoden bekannt sind. |
|
|
Did. Hinweise
|
Aufgabe
|
Material (Kopiervorlage)
|
Inhaltlich verantwortlich:
Andrea Neubauer, Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg)
Eingestellt am: 22.09.2020
Stand vom: 12.07.2023
Stand vom: 12.07.2023
Dieses Medium ist freies Lern- und Lehrmaterial im Sinne der UNESCO-Initiative Open Educational Ressources (OER) Details zu OER.
Sie dürfen diesen Beitrag entsprechend oben angegebener Lizenz verwenden, wenn Sie folgende Quellenangabe benutzen:
Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39792)
Petra Behling (Halle), PD Dr. Heike Hagelgans (Halle), Martin Heiler (Lützen), Katrin Tänzer (Merseburg) auf dem Bildungsserver Sachsen-Anhalt (http://www.bildung-lsa.de/index.php?KAT_ID=13638#art39792)
Lizenzangaben der eingebundenen Medien
 | Originalbild von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung Sachsen-Anhalt /Lizenz: CC BY-SA 4.0 | |
| Dokument von Landesinstitut für Schulqualität und Lehrerbildung /Lizenz: CC BY-SA 4.0 | |
Beitrag eingestellt von: Frau Andrea Neubauer
Telefon: +49 (0)345 2042 264
E-Mail: andrea.neubauer@sachsen-anhalt.de
Telefon: +49 (0)345 2042 264
E-Mail: andrea.neubauer@sachsen-anhalt.de
| Niveaubestimmende Aufgabe Sekundarschule | Mathematik |
| Schuljahrgang 9 (HSA) |
|
| Fachlehrplan | Daten und Zufall – Häufigkeitsverteilungen |
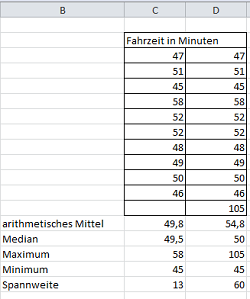
Häufigkeitsverteilungen
|
| KMK-Strategie Bildung in der digitalen Welt |
1.2 Auswerten und Bewerten 5.2 Werkzeuge bedarfsgerecht einsetzen |
|
| Aufgabentyp | Leistungsaufgabe | |
| Zeit | ca. 30 Minuten | |
| Produkt |
Testergebnis |
|
| Medien |
digitales Mathematikwerkzeug für jeden Lernenden (Tabellenkalkulation) |
|
| Aufgabenbeschreibung |
Diese Modellierungsaufgabe zielt darauf ab, grundlegende Kenngrößen unter Nutzung digitaler Werkzeuge zu berechnen und zu interpretieren. Dazu zählen die Berechnung des arithmetischen Mittels und der Spannweite sowie deren Interpretation in der Realsituation. |
|
|
Did. Hinweise
|
Aufgabe
|
Material (Kopiervorlage)
|